This question is about functional programming. It assumes prior knowledge in at least one purely functional language.

Question:

A polynomial $$ a_nx^n + a_{(n - 1)}x^{(n-1)} + \cdots + a_1x + a_0 $$ with integer coefficients \(a_0, a_1, \dots, a_n\) can be represented by a list or list-like structure (depending on the programming language of choice). For example, $$ p(x) = 5x^3 - 7x^2 + 2x + 10 $$ translates into the list [10, 2, -7, 5]. (From left to right, one starts with the constant term and finishes with the leading coefficient.) Now consider a function eval(), which takes an integer \(x_0\), and a list of coefficients \(a_0, a_1, \dots, a_n\), and evaluates the polynomial \(a_nx^n + \dots + a_1x + a_0\) at the point \(x_0\). Below are two implementations of this function, one in OCaml, and one in Haskell.

open Batteries

let eval : int -> int list -> int = fun x ->
  let rec ev i coeffs = 
    match coeffs with 
    | [] -> 0
    | (c :: cs) -> c*Int.pow x i + ev (i+1) cs 
  in ev 0

let main = (* calculate p(4) *)
  let p = [10; 2; -7; 5]
    in print_int (eval 4 p)

module Poly where

eval :: Int -> [Int] -> Int
eval x = ev 0 where 
  ev i coeffs = 
    case coeffs of
      [] -> 0
      (c:cs) -> c*x^i + ev (i+1) cs

p = [10, 2, -7, 5]

-- calculate p(4)
main = print (eval 4 p)

There is, however, a more efficient algorithm for this, known as Horner’s method. Using repeated application of the distributive law, we can derive the following sequence of progressive rearrangements of the expression: $$ a_0 + a_1x + \cdots + a_nx^n \\ = a_0 + x(a_1 + a_2x + \cdots + a_nx^{(n-1)}) \\ = a_0 + x(a_1 + x(a_2 + a_3x + \cdots + a_nx^{(n-2)})) \\ = a_0 + x(a_1 + x(a_2 + x(a_3 + \cdots + x(a_n + 0) \cdots ))) \\ $$

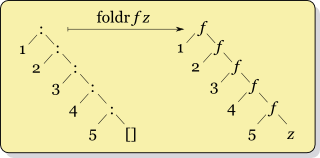
This lends itself naturally to a list processing pattern in functional programming, known as a fold. The fold (or reduce) family of higher-order functions reduces a collection to a single value using a combining function, and an initial value (named \(z\) in the below diagram).

In OCaml, List.fold_right has the type signature

('a -> 'b -> 'b) -> 'a list -> 'b -> 'b

and Haskell's foldr

foldr :: (a -> b -> b) -> b -> [a] -> b

(here specialized to lists) serves the same purpose.

Write, or sketch out, a function that

• behaves like (i.e., is extensionally equivalent to) eval() but
• takes advantage of Horner’s rule, and
• is implemented in terms of a right fold.

Toggle answer

eval' :: (Num a, Foldable t) => a -> t a -> a
eval' x = foldr1 f where f a c = a + x*c