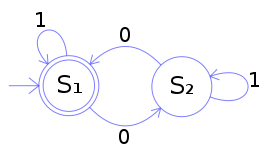
Here is a state diagram for a finite automaton which takes arbitrary binary strings as input. That is, a DFA defined over the binary alphabet \(\Sigma = \{0, 1\}\).

In simple terms, what is the behavior of this automaton? Or more formally: describe the language it accepts. How does the machine respond to the following input strings?
10011010111Write down the regular expression corresponding to the above DFA.
It accepts all strings with an even number of zeros. Of those in the list, only the last two are accepted. The equivalent regexp is /^((1*)0(1*)0(1*))*$/.